Basisbeispiel – Zylinderkondensator
Nachdem wir im ersten Artikel grundlegende Erkenntnisse zur Simulation und zu Isolierstoffen festgehalten haben, tauchen wir heute tiefer in die Simulation und Interpretation von Feldbildern ein. Mithilfe der Erkenntnisse, dass in diesem Blog-Artikel geschaffen wird, soll es in Zukunft möglich sein, Feldbilder zu verstehen und bspw. mit anderen Feldbildern vergleichen zu können.
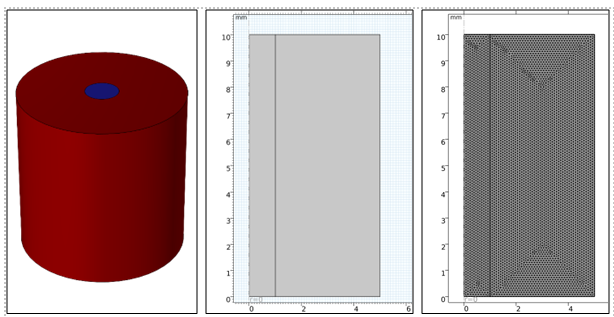
Den Anfang macht dabei das Beispiel des (unendlich langen und idealen) Zylinderkondensators (Abbildung 1) mit einem Dielektrikum. Die Ergebnisse der Simulation werden wir anschließend mit den theoretischen Berechnungsergebnissen vergleichen, weshalb wir zunächst die Grundlagen schaffen müssen.
Die herkömmliche Berechnung des Feldstärkeverlaufs innerhalb eines Zylinderkondensators (ohne Berücksichtigung der Enden des Kondensators) kann nach der Formel (1) durchgeführt werden. Eine Herleitung würde an dieser Stelle den Rahmen sprengen, die Formel selbst ist jetzt aus der Geometrie selbst hergeleitet und beschreibt das Verhalten der Feldstärke exakt. Die Feldstärke ist hierbei vom Radius r abhängig, weshalb es möglich ist für jeden Punkt zwischen den Elektroden (r1 und r2) einen exakten Wert für die Feldstärke E zu bestimmen.
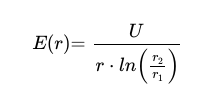
Die Radien der Elektroden bilden dabei die logischen Grenzen des Feldraums. Anhand der Darstellung der Gleichung kann man auch direkt die Form des Verlaufs erkennen: Die Feldstärke wird am Innenradius am höchsten sein und von dort nach außen sich in einem asymptotischen Verlauf der X-Achse annähern.
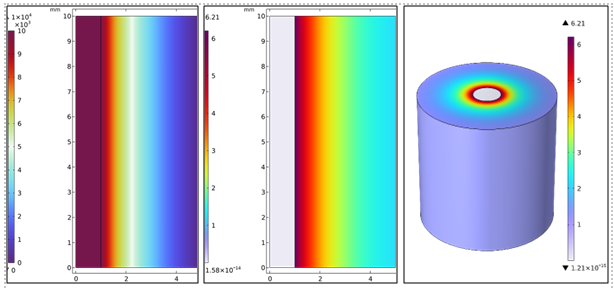
Springen wir nun in die Simulation und schauen uns ein paar Ergebnis-Plots in Abbildung 2 an.
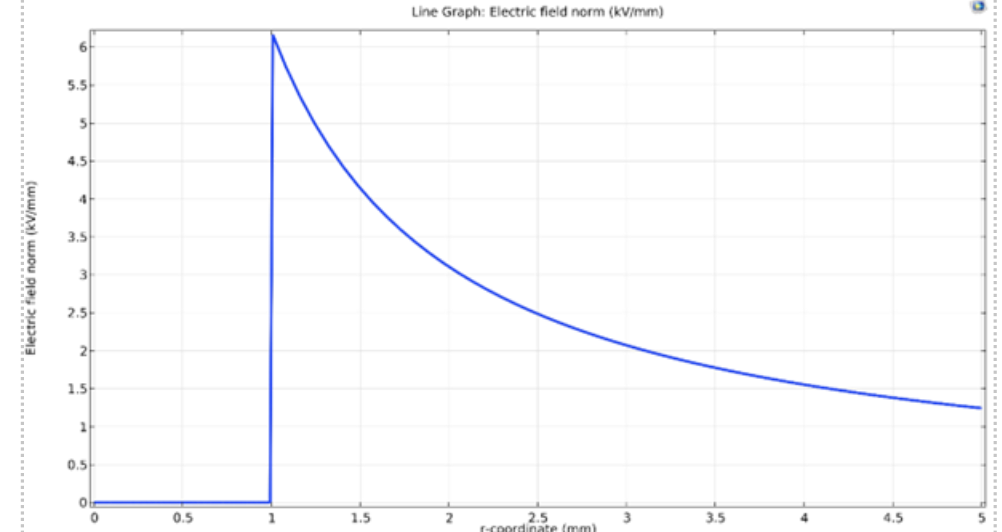
Aus den Grafiken lassen sich leicht die für die Simulation verwendeten Radien für Leiter und Dielektrikum ablesen: r1 ist 1 mm und r2 = 5 mm, die Spannung für dieses Beispiel wurde auf 10 kV festgelegt. Mit diesen Werten und der o.g. Formel lässt sich die Feldstärke für einen beliebigen Punkt innerhalb des Dielektrikums berechnen. Das Maximum wird direkt am Innenradius erreicht und erreicht einen Wert von 6,21 kV/mm. Erfreulicherweise ergibt die von der Simulation berechnete Maximalfeldstärke ebenfalls 6,21 kV/mm, was sowohl in Abbildung 2 als auch in Abbildung 3 gut zu erkennen ist. Auch der asymptotische Verlauf vom Innenradius zum Außenradius ist deutlich zu sehen.
Damit kommen wir für dieses Minimalbeispiel zunächst zum Ende. Wir konnten hier einen guten Bogen, zwischen Formel (Theorie) und Umsetzung (Simulation) spannen, sodass die bunten Grafiken in Abbildung 2 mithilfe des physikalischen Grundverständnisses interpretiert werden kann.
Spitze – Platte Geometrie?
Das zweite Beispiel führt die Inhomogene Feldverteilung im wahrsten Sinne auf die Spitze. Die Spitze-Platte Geometrie ist ein abstraktes Beispiel für stark inhomogene Bereiche in realen Anwendungen. In diesen Bereichen kommt man mit einer simplen
Ehom= UdEhom= Ud Abschätzung nicht weit und man wäre unweigerlich mit deutlich früheren Ausfällen der Isolation konfrontiert. Die Inhomogenität lässt sich durch den Ausnutzungsfaktor (oder Schwaigerfaktor) beschreiben und mit der homogenen Feldstärke multiplizieren (Formel (2)).
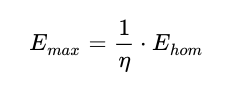
Dieser Faktor ist von vielen geometrischen Gegebenheiten abhängig und lässt sich in praktischen Anwendungen idR. nur experimentell ermitteln und ggf. durch empirische Formeln beschreiben. In einer beliebigen Geometrie, in der viele Parameter von den einfachen theoretischen Modellen abweichen, kann man ihn jedoch nicht ermitteln, oder die Formel zur Berechnung wird sehr komplex. Für eine Spitze-Platte Konfiguration wurde Formel (3) durch Experimente ermittelt, komplexere Elektroden-Anordnungen liefern nochmals deutlich anspruchsvollere Gleichungen. Auf die Details des Ausnutzungsgrads und der Formeln einzugehen, würde mehrere Blog-Posts füllen, weshalb an dieser Stelle nur die Gleichung an sich aufgeführt wird.
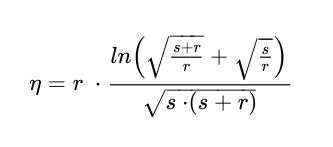
An dieser Stelle wird der Vorteil von Simulationen deutlich. Die Berechnung der physikalischen Größen wird hier nicht über den Schwaigerfaktor angenähert, sondern erfolgt durch die Geometrie und die Diskretisierung zusammen mit den gesetzten Randbedingungen. Zudem muss man nicht für jedes Modell und jede darin befindliche Elektrodenkonfiguration den entsprechenden Ausnutzungsgrad kennen, um eventuelle Schwächen in der Feldverteilung zu erkennen.
In Abbildung 4 sind zum einen die Geometrie mit den beiden Elektroden und zum anderen die Standardplots dargestellt. Die Nadel (Violett) hat einen Rundungsradius von 50µm und die Gegenelektrode ist 3mm entfernt. Im mittleren Bild ist die Potentialverteilung zu sehen, es fällt auf, dass fast das gesamte Potential innerhalb des ersten Millimeters abgebaut wird. Wie stark das Potential abfällt, lässt sich ebenfalls anhand des Feldstärkeplots (rechts) erkennen. Nahezu die komplette Feldstärkebelastung bündelt sich unmittelbar an der Spitze der Nadel und durch diese Bündelung wird der absolute Wert der Feldstärke so hoch, dass vermutlich jeder Isolierstoff in einem praxisnahen Kontext versagen würde.

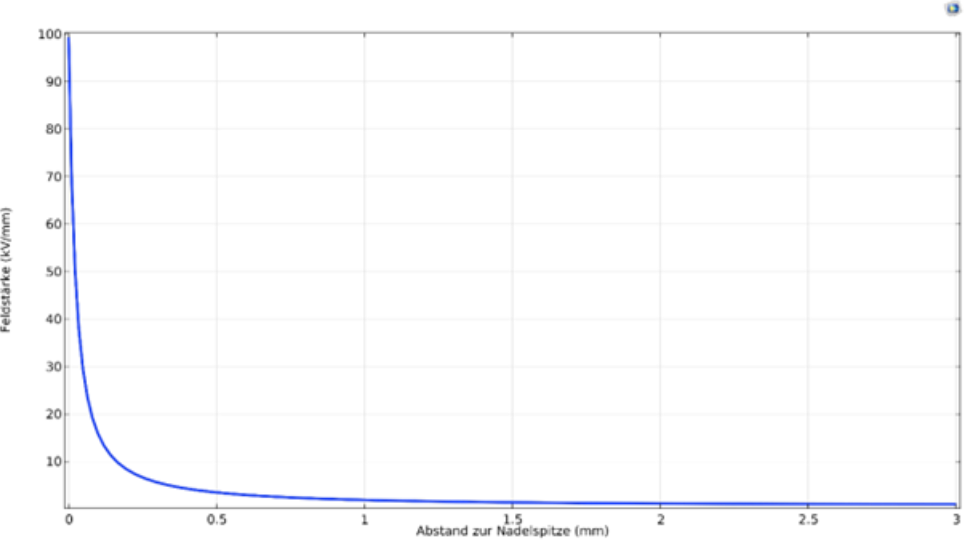
Ein genauer Blick auf den Feldstärkeverlauf (Abbildung 5) entlang der Rotationsachse (r=0mm), also genau von der Nadelspitze zur Platte vermittelt ein deutlicheres Bild über die Diskrepanz zwischen stark und schwach belastetem Feldraum. Innerhalb der ersten 0,5 mm fällt die Feldstärke vom Maximum auf unter 5%.
Es ist offensichtlich, dass eine derartige Feldverteilung in einer realen Anwendung unerwünscht ist.
Abschließende Bemerkungen
Warum sind diese Erkenntnisse wichtig?
Herkömmliche Isolierstoffe und stark inhomogene Anordnungen produzieren extreme, lokale Feldstärken. Bereits bei simplen Anwendungen, wie dem Zylinderkondensator (bspw. in Form eines HV-Kabels), können die Feldstärken am Innenradius deutlich überhöht sein, bei komplexeren Fällen, wie spitzen oder scharfen Kanten, erreicht diese Überhöhung so große lokale Feldstärken, dass die Isolierstoffe im Betrieb versagen können.
Was kann man dagegen machen?
In einfacheren Fällen genügt es die Geometrie der Elektroden und Oberflächen anzupassen, meist wird dies jedoch nicht möglich sein oder ausreichen. In diesen Fällen kann die Verwendung von nichtlinearen Isolierstoffen die lokalen Feldstärkeüberhöhungen abbauen und somit die Lebensdauer deutlich erhöhen.
Wie das aussieht und wie die NLCM in der Simulation funktionieren, sehen wir im nächsten Artikel dieser Blog-Serie.

