Basisbeispiel – Zylinderkondensator
Im letzten Blog-Eintrag dieser Serie haben wir uns zwei Basismodelle zum grundlegenden Verständnis für elektrische Felder und deren Simulation angesehen. Dabei konnten wir feststellen, dass theoretische Beschreibungen und Formeln für den praktischen Gebrauch zwar genutzt werden können, jedoch ab einer bestimmten Komplexität der Modelle nicht einfach „per Hand“ genutzt werden können. Diese Nutzbarkeit wird noch weiter reduziert, wenn wir nichtlinear-leitfähige Materialien (NLCM) verwenden.
Bereits im ersten Blog wurde erwähnt, dass die Nichtlinearität dieser Werkstoffe dafür sorgt, dass grundlegende Gleichungen, wie bspw. ![]() keine Anwendung mehr findet, da diese Formel eine lineare Funktion des Isolierstoffs voraussetzt.
keine Anwendung mehr findet, da diese Formel eine lineare Funktion des Isolierstoffs voraussetzt.
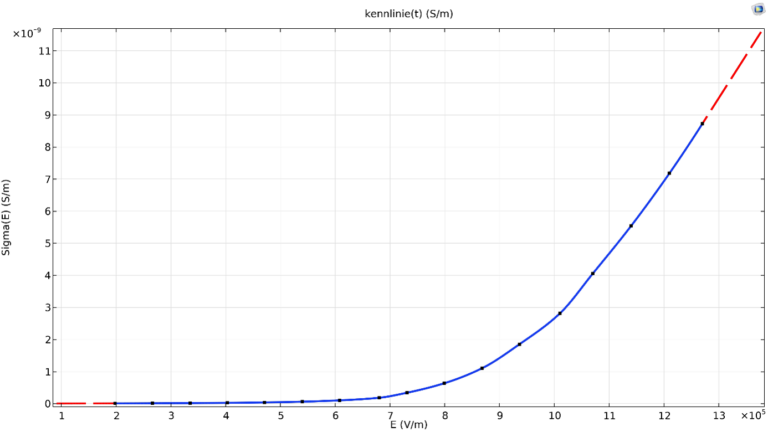
Deutlich wird dies bereits in unserem ersten heutigen Beispiel: Wir verwenden wieder den Zylinderkondensator von letzter Woche, doch statt einem linearen Isolierstoff nutzen wir eine nichtlineare Leitfähigkeitskennlinie. Die verwendete Kennlinie ist in Abbildung 1 dargestellt, dabei wurden die schwarzen Datenpunkte vorgegeben und über Comsol-eigene Funktionen Interpoliert (blau) sowie Extrapoliert(rot). Die Kennlinie zeig die Abhängigkeit der Leitfähigkeit (Sigma) von der angelegten Feldstärke (E), die im Material vorherrscht. Das Besondere bei der Simulation ist dann, dass für jeden Knotenpunkt des diskretisierten Feldraums die Leitfähigkeit in Abhängigkeit der Feldstärke anhand der Kennlinie berechnet wird.
Das Vorgehen ist nicht trivial, da bei der Berechnung keine direkte Lösung entsteht, sondern ein iterativer Prozess, bei dem sich der tatsächlichen Lösung des Feldes bis zu einer Fehlertoleranz angenähert wird.
Was bedeutet das?
Zuerst wird das Programm auf Basis der Randbedingungen für jeden Knoten eine erste Lösung für die Feldstärke ermitteln. Anschließend wird auf Basis dieser Feldstärke überprüft, inwiefern sich die Leitfähigkeit ändert. Durch die Änderung der Leitfähigkeit ergibt sich wiederum ggf. eine Veränderte vorliegende Feldstärke (aufgrund von Ausgleichprozessen im Material). Damit ist allerdings erneut die Feldstärke vom vorherigen Schritt verschieden, weshalb ein weiterer Schritt die neuen Werte mit der Kennlinie abgleicht.
Wie wir sehen, resultiert daraus ein iterativer Prozess, bei dem mit jedem Durchlauf die Leifähigkeitsänderung eine Änderung der Feldstärke hervorruft und diese Änderung wiederum eine Anpassung der Leitfähigkeit nach sich zieht. Physikalisch wird sich dieser Prozess so lange fortsetzen bis innerhalb des Materials ein energetisches Minimum für die Feldverteilung erreicht ist.
Was das für die Verteilung der Feldstärke im Beispiel des Zylinders heißt, lässt sich in den folgenden Grafiken (Abbildung 2) erkennen. Vergleicht man das linke und mittlere Bild, dann erscheint die Feldstärke im NLCM deutlich höher, beachtet man jedoch die Absolutwerte so fällt auf, dass die Maximalfeldstärke von 6,21 auf 3,83 kV/mm reduziert ist. Zusätzlich ist das gesamte Material nahezu gleichmäßig (homogen) belastet, was daran zu erkennen ist, dass die Feldstärke am rechten Rand bei ca. 2kV/mm liegt. Im Gegensatz dazu ist die Minimalfeldstärke im linearen Material bei etwa 1,2 kV/mm (Vgl. letzter Blog). Vergleicht man lineares und nichtlineares Material bei der gleichen Skalierung der Farbachse, dann fällt genau diese Homogenität deutlicher auf. Während das lineare Material beinahe das komplette Farbspektrum für die vorherrschenden Feldstärken nutzt, bewegt sich das Spektrum beim nichtlinearen Material nur im mittleren Bereich.

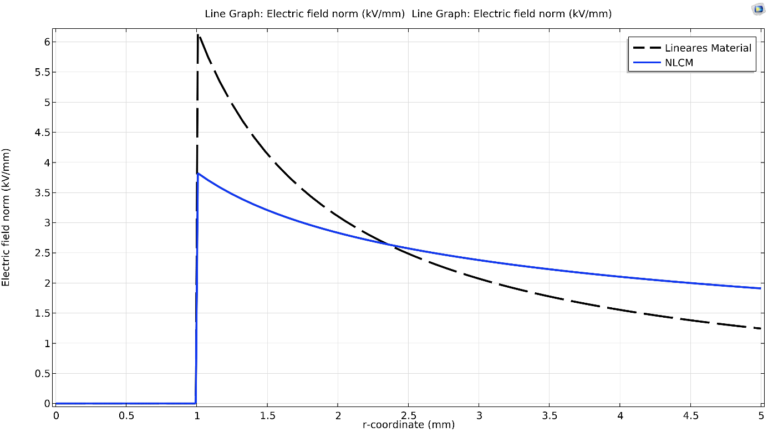
Nutzen wir die Auswertung mittels Feldstärke-Graphen (Abbildung 3), der entlang des Radius vom Zentrum zum Außenleiter, so kann man den nichtlinearen Glättungseffekt noch deutlicher erkennen. Die inhomogene Verteilung aufgrund der Geometrie wird beim NLCM sehr stark geglättet, sodass beinahe ein homogener Verlauf entsteht. Auch hier kann man sehen, dass die Feldstärke beim nichtlinearen Material zwischen Innenleiter und Außenleiter nicht so stark abfällt (ca. 3,8kV/mm auf 1,9kV/mm), wie das verglichen dazu beim linearen Material der Fall ist (6,2kV/mm auf 1,2kV/mm).
Spitze – Platte Geometrie?
Schließen wir nun den Bogen zum letzten Blog und begeben uns zur Spitze-Platte Geometrie. Die um ein Vielfaches stärkere Inhomogenität dieses Modells erschwert bestimmte Betrachtungen beim direkten Vergleich zwischen den beiden Materialarten. Für ein einheitliches Bild des Blogs wird aber das einmal eingeführte Konzept fortgesetzt.
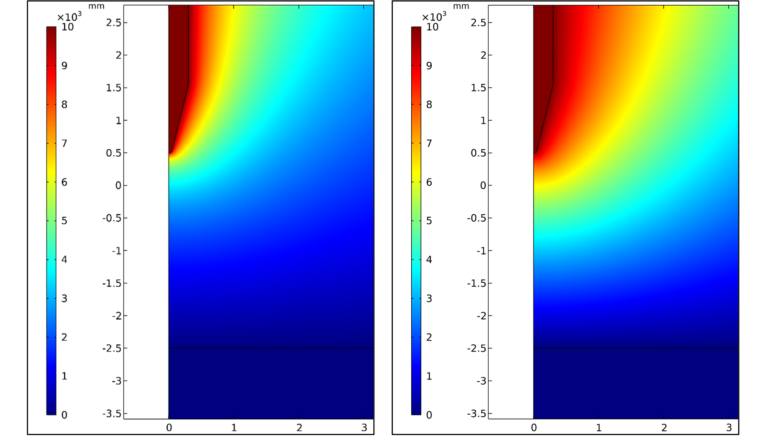
Die Materialdaten sind exakt die gleichen, wie im Zylinderkondensator-Modell und alle physikalischen Randbedingungen wurden ebenfalls beibehalten. Die ersten Vergleiche zwischen linearem und nichtlinearem Material führen wir am besten bei der Potentialverteilung (Abbildung 4) durch. Die Unterschiede auf den Konturplots sind auf den ersten Blick nicht einfach festzustellen, jedoch ist die Potentialverteilung am aussagekräftigsten. Die Skalierung ist in beiden Berechnungen identisch und der Bildausschnitt ist ebenfalls gleich. Es fällt auf, dass die „Potentialwolke“ mit höheren Spannungen (>4kV) beim NLCM (rechtes Bild) deutlich voluminöser ausgeprägt ist. Dass dies ein gut ist, mag im ersten Moment kontraintuitiv sein, ist jedoch beim zweiten Blick tatsächlich ein Vorteil. Es bedeutet, dass das Potential nicht innerhalb des ersten Millimeters nahezu vollständig abgebaut wird, wie im letzten Blog festgestellt. Stattdessen wird hier über einen deutlich größeren Bereich und damit gleichmäßiger das Potential gesteuert, was sich letztlich auch auf die Feldstärke(-verteilung) auswirkt. Als Vergleich hierzu könnte der ideale Plattenkondensator zurate gezogen werden. Bei diesem wird auch das Potential gleichmäßig und gleichförmig über die komplette Isolierstrecke abgebaut, wodurch auch das elektrische Feld homogen ist.
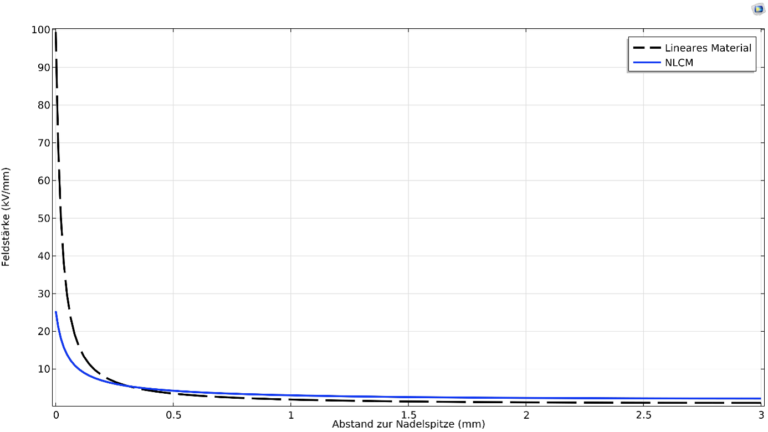
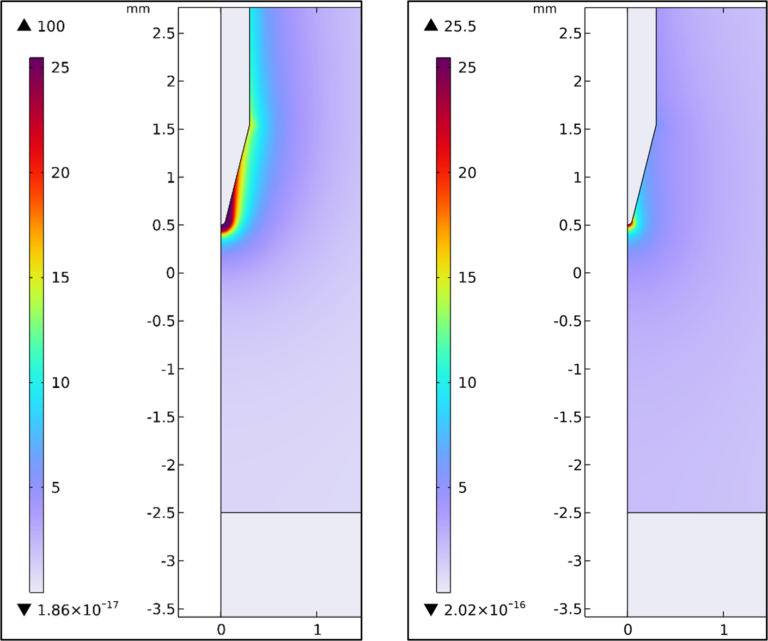
Zum Vergleich der elektrischen Feldverteilung (Abbildung 5) können wir die deutlichen Unterschiede sichtbar machen, indem wir die Skalierung auf das Ergebnis mit der geringeren Maximalfeldstärke normieren. Dadurch werden die Bereiche hervorgehoben, die über dem Maximum der Skala liegen. Die geringere Maximalfeldstärke liegt in der Berechnung mit dem nichtlinearen Material vor. Die Absolutwerte der berechneten Maxima liegen deutlich auseinander: 25kV/mm beim NLCM und 100kV/mm beim linearen Isolierstoff. Ein Faktor von 4 bei den Maximalwerten spricht für sich, wenn auch das Szenario hier nicht praxisnah ist.
Ein zusätzlicher Blick auf den Feldstärkeverlauf zwischen Spitze und Platte in Abbildung 6 zeigt noch einmal ganz deutlich, wie die Funktion des NLCM wirkt. Die hohen Feldstärkewerte direkt an der Spitze werden drastisch reduziert und gleichzeitig wird der hintere Bereich bis zur Plattenelektrode leicht mehr belastet. Auch hier wird insgesamt der Feldverlauf etwas mehr homogenisiert.
Abschließende Bemerkungen
Was haben wir heute gelernt?
Im heutigen Blog haben wir den direkten Vergleich zwischen herkömmlichen Isolierstoffen und NLCM anhand der Basismodelle aus dem letzten Blog gezogen. Wir konnten sehen, dass durch die Nichtlinearität die Feldstärke insgesamt deutlich geglättet wird und hohe Spitzenwerte stark reduziert werden. Diese Reduktion erhöht insgesamt die Lebensdauer und Festigkeit der Isolierstoffe und durch die gleichmäßigere Belastung allgemein die Zuverlässigkeit des Materials.
Je nach Materialkennlinie und Inhomogenität der Elektrodenkonfiguration erreicht man eine hohe „Deckelung“ der Maximalfeldstärke verglichen mit herkömmlichen Isolierstoffen, in unseren Beispielen waren Faktoren von 2 bis 4 möglich.
Wofür sind diese Erkenntnisse nun hilfreich?
Die Stärke und die Art und Weise der Feldsteuerung sind von Anwendung zu Anwendung verschieden, die hier vorgestellten Basisbeispiele sind von der geometrischen Komplexität sehr reduziert. In der Praxis helfen uns diese Ergebnisse abzuschätzen an welchen Stellen der Einsatz von NLCM sinnvoll ist. Durch die nichtlineare Materialkennlinie braucht es jedoch für eine endgültige Bestimmung der Feldstärken eine Feldsimulation.
Welche Fallstricke es bei der Simulation zu beachten gilt und wie die NLCM eingebunden werden, sehen wir dann im nächsten Blogeintrag zur Serie: „Funktionsweise nichtlinearer Isolierstoffe“

