Welche Daten werden benötigt?
In den letzten Blogeinträgen haben wir uns Grundlagen und einfache Beispiele mit und ohne NLCM angesehen. Im letzten Beitrag wurde bereits kurz auf die Kennlinie des Materials eingegangen. Diese und andere Eigenschaften werden nun in diesem Blogbeitrag etwas genauer unter die Lupe genommen und erklärt, wie und wieso sie in der Software benötigt werden.
Um welche Eigenschaften geht es denn genau? Nun, hier kommt es ganz speziell natürlich auf die gewünschten Simulationen und betrachteten physikalischen Gesetzmäßigkeiten an. Als Minimalanforderungen sind hier die elektrische Leitfähigkeit (oft durch das Formelzeichen σ repräsentiert) sowie die relative Permittivität (εr) zu nennen. Mit diesen beiden Größen können Isolierstoffe im elektrostatischen, quasistatischen und transienten E-Feld bestimmt werden. Wenn also Erwärmung, mechanische Beanspruchung oder weitere physikalische Phänomene vernachlässigt werden können, reichen die beiden genannten Materialparameter aus.
Im Zuge dieses Blogs bleiben wir auch bei den beiden Größen. Sollten bspw. thermische Parameter notwendig sein, werden mitunter andere Eigenschaften deutlich komplexer, was auch die Implementierung in die Software verkompliziert.
Permittivität
Die Permittivität ist in Isolieranordnungen von sehr großer Bedeutung. Sie bestimmt Verschiebungsströme und -felder und beeinflusst maßgeblich die Feldverteilung zwischen den verschiedenen Dielektrika (sofern vorhanden).
Die Permittivität des Materials kann bspw. über Kapazitätsmessungen ermittelt werden. Je nach Einsatzgebiet, kann es sein, dass dieser Wert keine Konstante ist. Bei der Messung und der Implementierung in die Software muss das natürlich beachtet werden. Für die meisten Isolierstoffe gilt dieser Wert in den technisch üblichen Bereichen als konstant.
Elektrische Leitfähigkeit
Die zentrale Eigenschaft der NLCM – die nichtlineare Leitfähigkeit – ist für die Simulation ebenfalls eine Kerneigenschaft. Ermittelt wird sie über die Messung der U-I-Kennlinie (oder auch Widerstandskennlinie genannt). Es wurde bereits erwähnt, dass im Gegensatz zu herkömmlichen Isolierstoffen bei dieser Kennlinie keine Gerade, sondern eine Kurve messbar ist. Eine Gerade würde einem (konstanten) Quotienten von Spannung und Strom (dem Widerstand) entsprechen. Die Nichtlinearität hingegen, sorgt dafür, dass dieser Quotient nicht über den kompletten Spannungsbereich konstant bleibt, sondern stark variiert. Dieser nichtlineare Zusammenhang resultiert darin, dass die Leitfähigkeit bei sehr geringen Feldstärken sehr gering bleibt (vergleichbar mit einem reinen Isolierstoff). Steigt die Feldstärke jedoch an, bilden sich im Material leifähige Pfade aus, sodass die Leitfähigkeit ansteigt. Charakteristisch erhält die Kennlinie bei einer bestimmten Feldstärke einen „Knick“, ab dem die Leitfähigkeit rapide ansteigt. Die resultierende Kennlinie ist vergleichbar mit der typischen Diodenkennlinie.
Aus der gemessenen I-U-Kennlinie kann anschließend eine J-E-Kennlinie berechnet werden. Hierzu werden geometrieabhängige Größen, wie Elektrodenfläche und Abstände zu den jeweiligen elektrischen Größen Strom und Spannung hinzugezogen, um die Stromdichte J und die Feldstärke E zu bestimmen. Ggf. werden noch Korrekturfaktoren (siehe Schwaiger-Faktor) zu Rate gezogen, um evtl. vorhandene Inhomogenitäten herauszurechnen. Aus diesem Vorgehen wird auch ersichtlich, dass man die Kennlinie bei einer möglichst homogenen Elektrodenanordnung ermitteln sollte. Die Korrekturfaktoren für Inhomogenität des Feldes und der effektiven Elektrodenfläche (durch welche der Strom fließt) sollten einfach beschreib- und bestimmbar sein.
Anschließend kann man die J-E-Kennlinie in eine σ-E-Kennlinie umrechnen, indem für die y-Werte σ=J/E verwendet wird.
Einbinden in die Software
Die Materialdaten in COMSOL einzubinden ist ein recht simpler Prozess, wohingegen der Ablauf der Simulation und der mathematisch-physikalische Hintergrund beliebig kompliziert werden kann. Eine Beurteilung der Validität der Simulationsergebnisse kann jedoch nur erfolgen, wenn die Hintergründe hinreichend bekannt sind.

Ein neues (Blanko-)Material besitzt keine Eigenschaften. Die Liste mit Materialeigenschaften („properties“) ist leer und kann auch einer langen Liste an möglichen Eigenschaften definiert werden (siehe Abbildung 1). Wie bereits erwähnt, kommt es auf das Simulationsmodell an, welche Eigenschaften definiert werden müssen, damit das Programm überhaupt rechnen kann. „Relative permittivity“ und „Electrical conductivity“ sind die beiden Eigenschaften, auf die es im Rahmen dieses Blogs ankommt, weshalb sie in Abbildung 1 unter „Output Properties“ bereits gelistet sind. Die einheitenlose relative Permittivität wurde mit einem konstanten Wert versehen, während die Leitfähigkeit auf eine Kennlinie (mit dem Namen „kennlinie“) zurückgreift. Diese Kennlinie soll die o.g. σ-E-Kennlinie sein, die aus unseren Messwerten abgeleitet wurde. In dieser ist die Leitfähigkeit eine vom E-Feld abhängige Größe und dieser Sachverhalt wird in dem Eintrag unter „Expression“ mit berücksichtigt, indem gesagt wird, dass die Kennlinie von „ec.normE“ abhängig ist. Dies ist die Comsol-eigene Bezeichnung für eine spezielle Variable, die das Programm intern ermittelt bzw. auf die der User zugreifen kann. „ec“ steht dabei für das Interface, dass für die Simulation genutzt wird: electric currents ausgeschrieben. Dieses Interface erlaubt die Nutzung des frequenzabhängigen Teils der Feldgleichung und den dazugehörenden Materialeigenschaften. „normE“ steht für den normierten Wert des Elektrischen Feldes (in einem konkreten Punkt im Feldraum), also dem Betrag des E-Feld-Vektors an einem Knotenpunkt des Meshs.
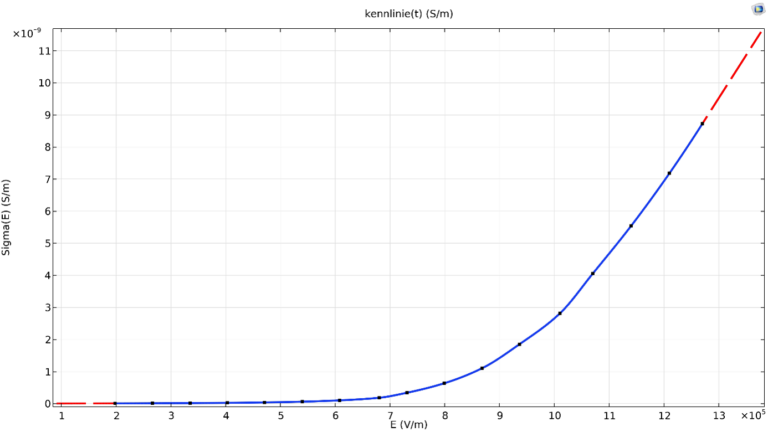
Im nächsten Schritt wird die Funktion „kennlinie“ mit entsprechenden Daten versehen. Dies kann bspw. eine Funktionsgleichung oder eine Wertetabelle sein. Für unser Beispiel nutzen wir eine Werte-Tabelle, die auf den gemessenen und umgerechneten Werten der I-U-Kennlinie basieren. COMSOL nutzt an dieser Stelle t als Argument der Funktion f(t). Je genauer die Daten sind und je exakter die Inter- und Extrapolation das reale Materialverhalten abbilden, desto realistischer sind auch die Ergebnisse der Simulation. Gerade das Verhalten der Extrapolation beeinflusst sehr stark, wie das Material außerhalb der gemessenen Kennlinie arbeitet.
Normalerweise kann Comsol bei linearen Materialien zur Lösung der Feldgleichungen einen direkten „Solver“ nutzen. Das bedeutet, dass eine große Matrix für die Feldgleichungen aufgesetzt werden kann, die die Lösungen für die einzelnen Knotenpunkte des Meshs liefert (Beispiel für Mesh siehe Blogartikel 2). Durch die geringe Komplexität eines linearen Gleichungssystems ist dieser Solver in der Lage in relativ kurzer Zeit eine Lösung für die Feldgleichungen zu liefern. Bei der Verwendung nichtlinearer Materialien kann dieser Ansatz jedoch nicht mehr verwendet werden, weil die Ergebnisse eines Knotenpunktes die Ergebnisse der benachbarten Knoten beeinflusst. Aus diesem Grund muss die Berechnung bei NLCM iterativ erfolgen. Dabei wird die gesamte Feldgleichungsmatrix mehrmals berechnet, wobei der vorherige Berechnungsschritt als Ausgangspunkt für den nächsten genutzt wird. Dieser Prozess wird so lange durchgeführt, bis eine gewisse Fehlertoleranz erreicht wird, oder abgebrochen, sobald eine bestimmte Anzahl an Iterationsschritten nicht zum Erfolg führte.
3 Abschließende Bemerkungen
In der heutigen Ausgabe des Blogs über nichtlinear leitfähige Materialien haben wir geklärt, welche Materialeigenschaften von Bedeutung sind und wie sie in der Software eingebunden werden. Zusätzlich wurden Hürden aufgezeigt, bei denen die Simulation an Ihre Grenzen stößt, wenn die Parameter nicht sorgfältig definiert werden. Im nächsten Blogartikel stürzen wir uns nun auf die tatsächliche Funktionsweise der NLCM und schauen uns Konzepte an, mit denen wir das Verhalten beschreiben können.

